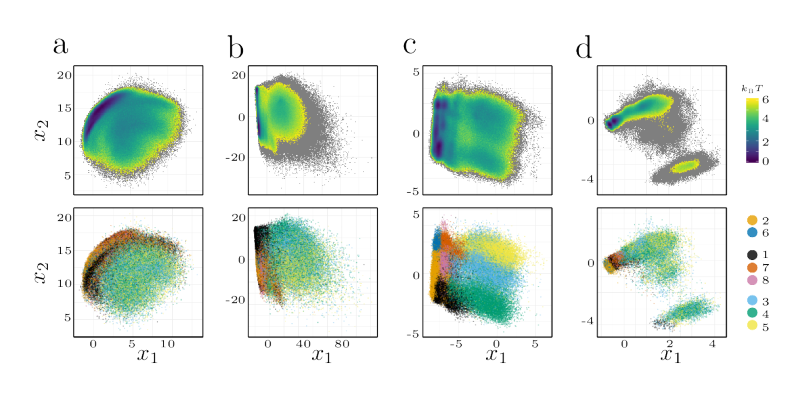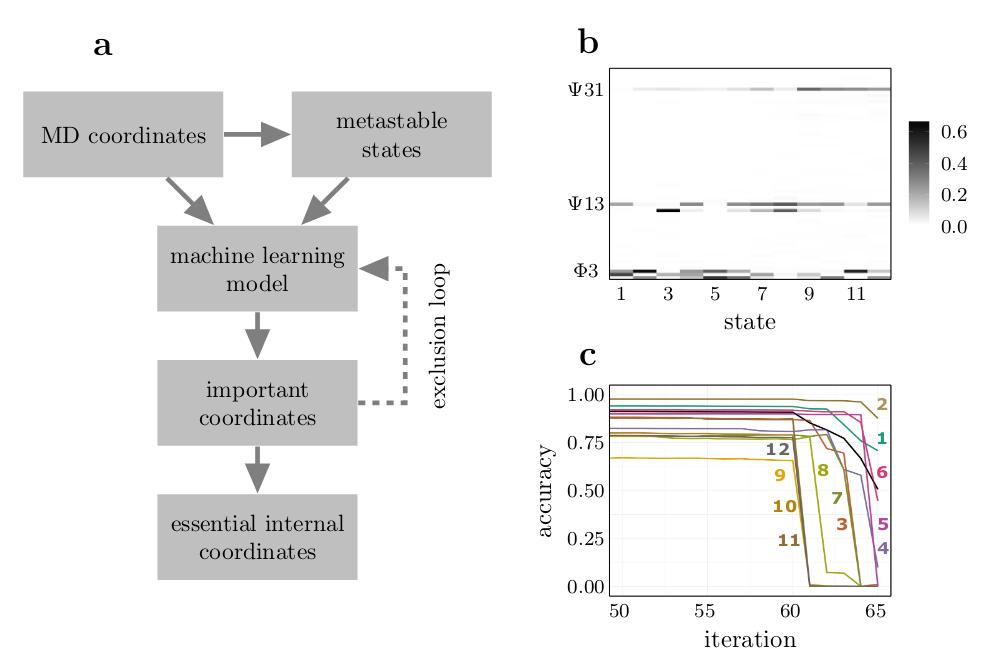Our Research

Here are some (but not all) of our research interests. For more information, please visit the publications page.

Combining single molecule FRET measurements and MD simulations to elucidate hierachical dynamics in allostery

We report on a study that combines advanced fluorescence methods with molecular dynamics (MD) simulations to cover timescales from nanoseconds to milliseconds for a large protein. This allows us to delineate how ATP hydrolysis in a protein causes allosteric changes at a distant protein binding site, using the chaperone Hsp90 as test system. The allosteric process occurs via hierarchical dynamics involving timescales from nano- to milliseconds and length scales from Ångstroms to several nanometers. We find that hydrolysis of one ATP is coupled to a conformational change of Arg380, which in turn passes structural information via the large M-domain α-helix to the whole protein. The resulting structural asymmetry in Hsp90 leads to the collapse of a central folding substrate binding site, causing the formation of a novel collapsed state (closed state B) that we characterise structurally. We presume that similar hierarchical mechanisms are fundamental for information transfer induced by ATP hydrolysis through many other proteins.
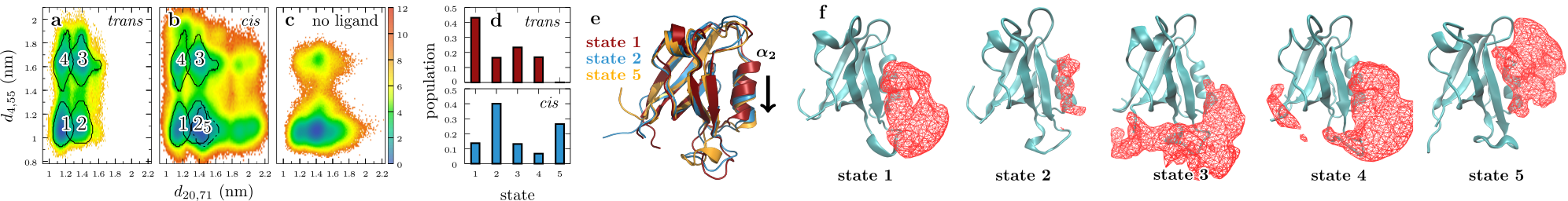
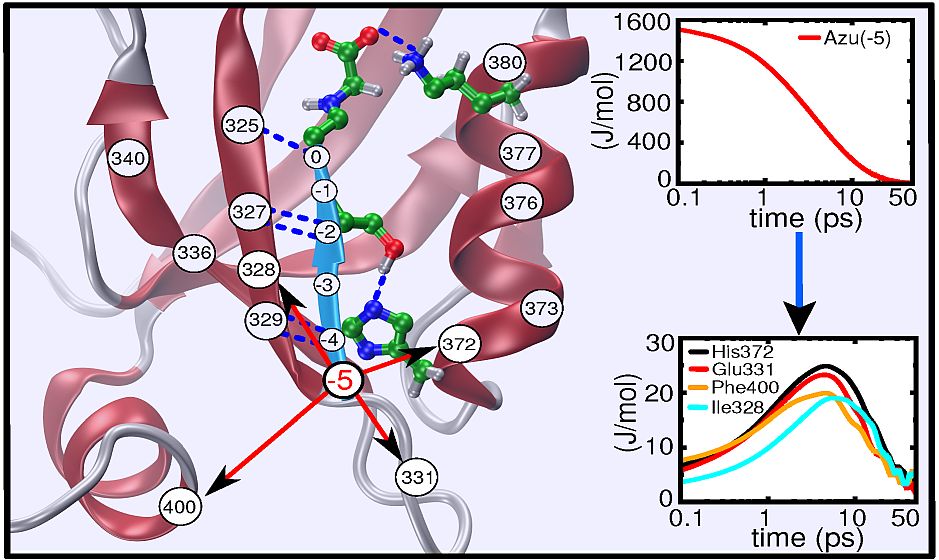
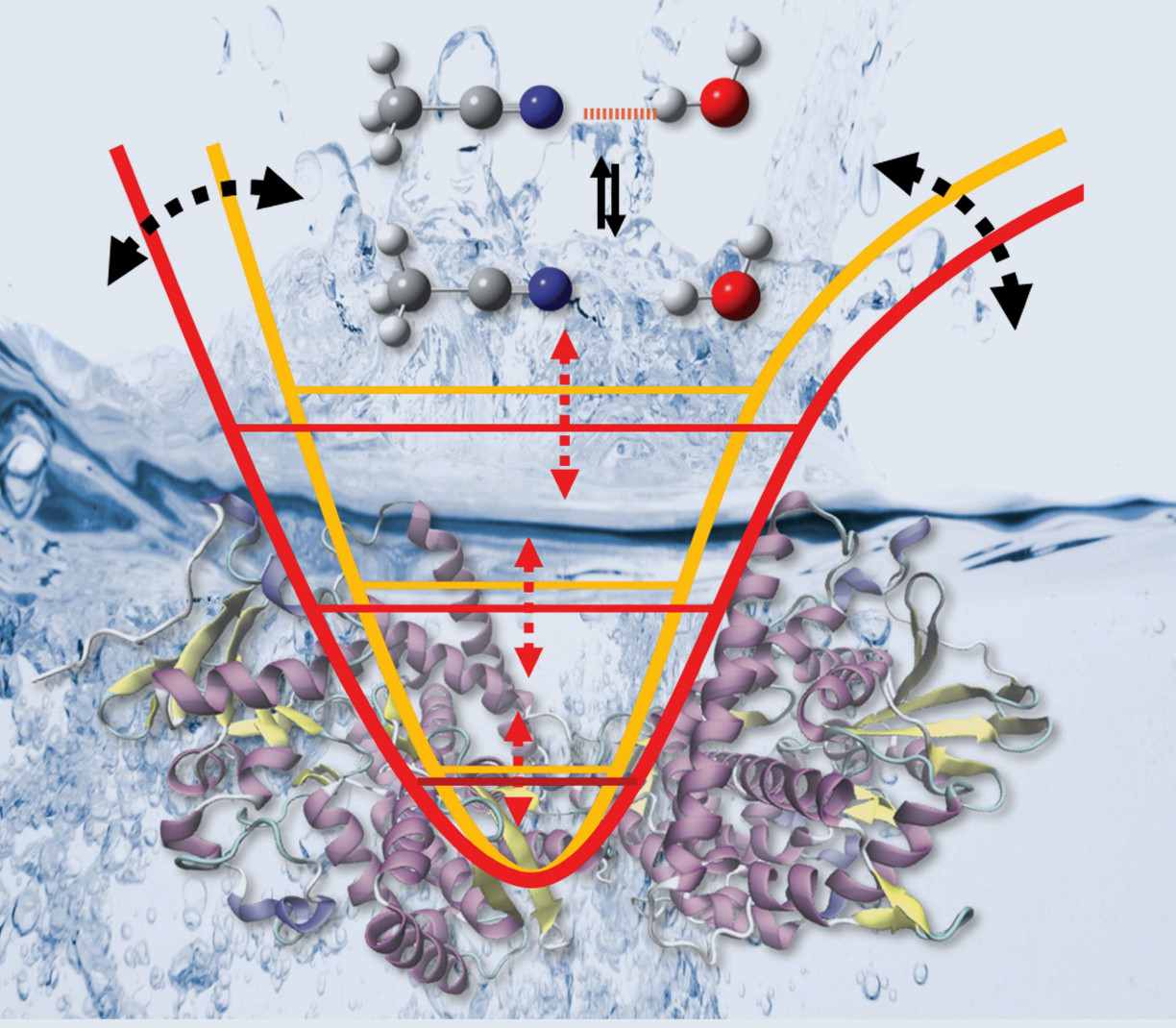
• Hierarchical dynamics in allostery following ATP hydrolysis monitored by single molecule FRET measurements and MD simulations S. Wolf, B. Sohmen, B. Hellenkamp, J. Thurn, G. Stock, and T. Hugel, Chem. Sci., 1–10 (2021)

Real-time observation of ligand-induced allosteric transitions

While allostery is of paramount importance for protein regulation, the underlying dynamical process of ligand (un)binding at one site, resulting time evolution of the protein structure, and change of the binding affinity at a remote site is not well understood. Here the ligand-induced conformational transition in a widely studied model system of allostery, the PDZ2 domain, is investigated by transient infrared spectroscopy accompanied by molecular dynamics simulations. To this end, an azobenzene derived photoswitch is linked to a peptide ligand in a way that its binding affinity to the PDZ2 domain changes upon switching, thus initiating an allosteric transition in the PDZ2 domain protein. The subsequent response of the protein, covering four decades of time ranging from ~1ns to ~10μs, can be rationalize by a remodelling of its rugged free energy landscape, with very subtle shifts in the populations of a small number of structurally well defined states. It is proposed that structurally and dynamically driven allostery, often discussed as limiting scenarios of allosteric communication, actually go hand-in-hand, allowing the protein to adapt its free energy landscape to incoming signals.
• Real-time observation of ligand-induced allosteric transitions in a PDZ domain, Olga Bozovic, Claudio Zanobini, Adnan Gulzar, Brankica Jankovic, David Buhrke, Matthias Post, Steffen Wolf, Gerhard Stock, Peter Hamm, PNAS 117, 26031 (2020), arXiv:2008.01625

Nonequilibrium MD simulations of a proteins allosteric communication

Allostery represents a fundamental mechanism of biological regulation that is mediated via long-range communication between distant protein sites. Although little is known about the underlying dynamical process, recent time-resolved infrared spectroscopy experiments on a photoswitchable PDZ domain (PDZ2S) have indicated that the allosteric transition occurs on multiple timescales. Here, using extensive nonequilibrium molecular dynamics simulations, a time-dependent picture of the allosteric communication in PDZ2S is developed. The simulations reveal that allostery amounts to the propagation of structural and dynamical changes that are genuinely nonlinear and can occur in a nonlocal fashion. A dynamic network model is constructed that illustrates the hierarchy and exceeding structural heterogeneity of the process. In compelling agreement with experiment, three physically distinct phases of the time evolution are identified, describing elastic response (≲0.1 ns), inelastic reorganization (∼100 ns), and structural relaxation (≳1μs). Issues such as the similarity to downhill folding as well as the interpretation of allosteric pathways are discussed.
• Time-resolved observation of protein allosteric communication, Sebastian Buchenberg, Florian Sittel, and Gerhard Stock, PNAS 114, 33, E6804 (2017)
Energy transport through molecular systems has recently received considerable interest, in particular, due to its importance for molecular electronics and the functioning of biological systems. In experiment, energy is usually induced into the molecule by photoexcitation of a chromophore or by pumping a localized infrared vibration. This triggers an cascade of dynamical processes including
  • the femtosecond vibrational energy redistribution from localized high-frequency modes to delocalized low-frequency modes,
  • transport of energy through the molecule, and
  • the cooling the molecules due to heat transfer to the solvent.
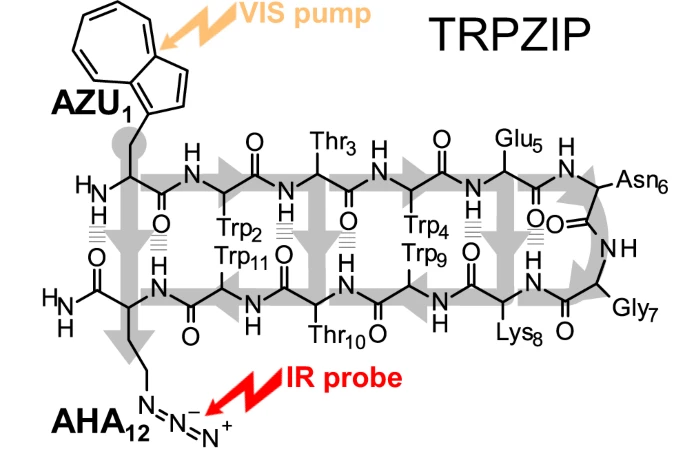
To study these processes in biomolecules such as peptides, proteins, and RNA, we combine quantum-classical techniques well-known from the description of gas phase reactions with biomolecular force fields typically used in all-atom molecular dynamics simulations. This leads to nonequilibrium molecular dynamics simulations, which mimic the laser excitation of the molecules by nonequilibrium phase-space initial condition for the solute and the solvent atoms. To understand the quantum effects involved, we furthermore perform classical and quantum-mechanical perturbation theory. The results are discussed in the light of recent time-resolved infrared experiments.

Through Bonds or Contacts? Mapping Protein Vibrational Energy Transfer Using Non-canonical Amino Acids

We examine vibrational energy flow in dehydrated and hydrated villin headpiece subdomain HP36 by master equation simulations. Transition rates used in the simulations are obtained from communication maps calculated for HP36. In addition to energy flow along the main chain, we identify pathways for energy transport in HP36 via hydrogen bonding between residues quite far in sequence space. The results of the master equation simulations compare well with all-atom non-equilibrium simulations to about 1 ps following initial excitation of the protein, and quite well at long times, though for some residues we observe deviations between the master equation and all-atom simulations at intermediate times from about 1–10 ps. Those deviations are less noticeable for hydrated than dehydrated HP36 due to energy flow into the water.
• Through Bonds or Contacts? Mapping Protein Vibrational Energy Transfer Using Non-canonical Amino Acids E. Deniz, L. Valiño-Borau, J. Löffler, K. Eberl, A. Gulzar, S. Wolf, P. Durkin, R. Kaml, N. Budisa, G. Stock, J. Bredenbeck, Nat. Commun. 12, 3284 (2021)

Master equation model to predict energy transport pathways in proteins

Recent time-resolved experiments and accompanying molecular dynamics simulations allow us to monitor the flow of vibrational energy in biomolecules. As a simple means to describe these experimental and simulated data, Buchenberg et al. [J. Phys. Chem. Lett. 7, 25 (2016)] suggested a master equation model that accounts for the energy transport from an initially excited residue to some target residue. The transfer rates of the model were obtained from two scaling rules, which account for the energy transport through the backbone and via tertiary contacts, respectively, and were parameterized using simulation data of a small α-helical protein at low temperatures. To extend the applicability of the model to general proteins at room temperature, here a new parameterization is presented, which is based on extensive nonequilibrium molecular dynamics simulations of a number of model systems. With typical transfer times of 0.5–1 ps between adjacent residues, backbone transport represents the fastest channel of energy flow. It is well described by a diffusive-type scaling rule, which requires only an overall backbone diffusion coefficient and interatom distances as input. Contact transport, e.g., via hydrogen bonds, is considerably slower (6–30 ps) at room temperature. A new scaling rule depending on the inverse square contact distance is suggested, which is shown to successfully describe the energy transport in the allosteric protein PDZ3. Since both scaling rules require only the structure of the considered system, the model provides a simple and general means to predict energy transport in proteins. To identify the pathways of energy transport, Monte Carlo Markov chain simulations are performed, which highlight the competition between backbone and contact transport channels.
• Master equation model to predict energy transport pathways in proteins L. Valiño Borau, A. Gulzar, and G. Stock, J. Chem. Phys. 152, 045103 (2020)

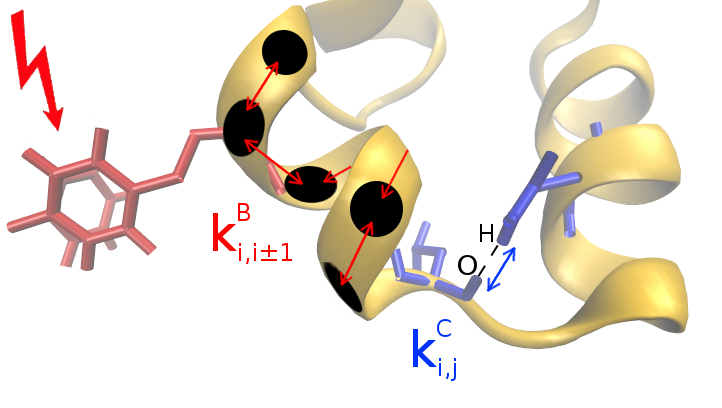
Scaling Rules for Energy Transport

We examine vibrational energy flow in dehydrated and hydrated villin headpiece subdomain HP36 by master equation simulations. Transition rates used in the simulations are obtained from communication maps calculated for HP36. In addition to energy flow along the main chain, we identify pathways for energy transport in HP36 via hydrogen bonding between residues quite far in sequence space. The results of the master equation simulations compare well with all-atom non-equilibrium simulations to about 1 ps following initial excitation of the protein, and quite well at long times, though for some residues we observe deviations between the master equation and all-atom simulations at intermediate times from about 1–10 ps. Those deviations are less noticeable for hydrated than dehydrated HP36 due to energy flow into the water.
• Scaling Rules for Vibrational Energy Transport in Globular Proteins S. Buchenberg, D. M. Leitner, and G. Stock, J. Phys. Chem. Lett. 7, 25 (2016)
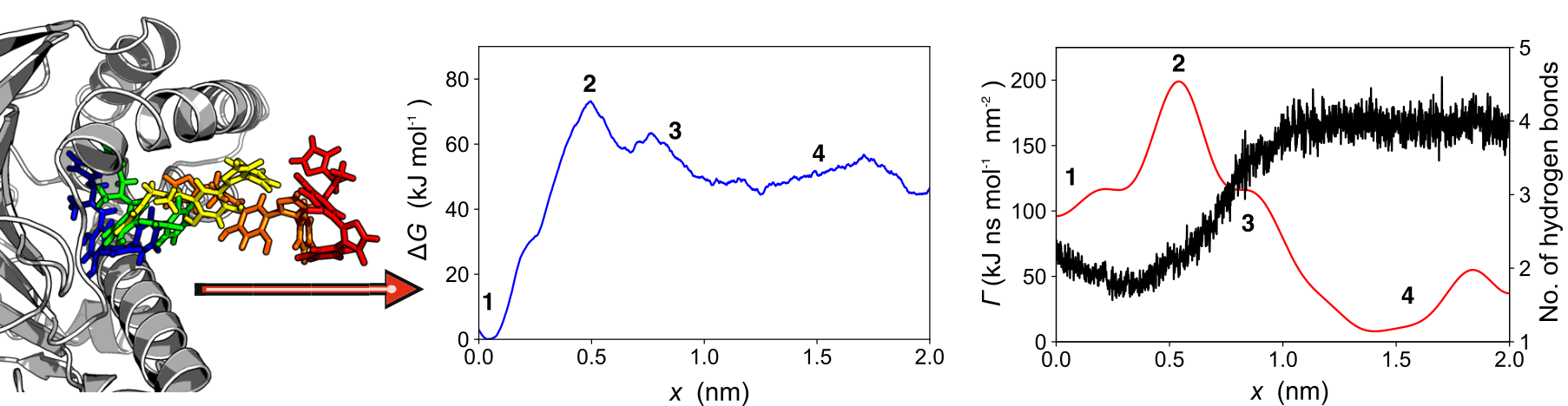
While common molecular dynamics simulation methods are capable to simulate molecular processes on timescales up to milliseconds, the biologically relevant range of timescales reaches from microseconds to minutes. To enforce structural changes on such timescales, biased MD simulation methods have been developed, which aim at predicting free energies along a predefined reaction coordinate. A problem with this type of simulation and analysis is that the resulting free energies only allow limited inference of the unbiased systems's dynamics and nonequilibrium effects such as dissipation, as fast degrees of freedom have been integrated out. To allow such a coarse-graining of system dynamics, we have developed dissipation-corrected targeted molecular dynamics. Combining the Jarzynski equality and the Markovian Langevin equation, we derive an expression for a dissipation correction that can be calculated on-the-fly for nonequilibrium pulling simulations. Our approach does not only result in the free energy profile, but in friction factors, as well, the latter allowing insights into fast dynamics and fluctuations along the biasing coordinate as well as their molecular origin. Furthermore, both quantities can serve as input for integration of a Langevin equation, speeding up calculations of system dynamics by several orders of magnitude. Combination with our approach of temperature boosted Langevin equation simulations finally allows to access timescales of up to minutes.
• Targeted Molecular Dynamics Calculations of Free Energy Profiles Using a Nonequilibrium Friction Correction, S. Wolf and G. Stock, J. Chem. Theory Comput 12, 6175 (2018)
• Multisecond ligand dissociation dynamics from atomistic simulations, S. Wolf, B. Lickert, S. Bray, and G. Stock, Nat. Commun. 11, 2918 (2020)

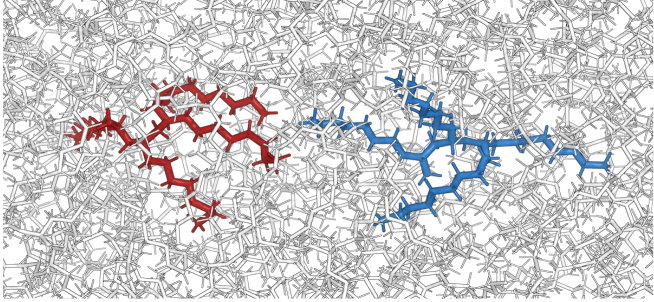
Molecular Origin of Driving-Dependent Friction in Fluids

The friction coefficient of fluids may become a function of the velocity at increased external driving. This non-Newtonian behavior is of general theoretical interest as well as of great practical importance, e.g., for the design of lubricants. Using dissipation-corrected targeted molecular dynamics, we pull apart two tagged liquid molecules in the presence of surrounding molecules to study this driving-dependence of the friction. Describing the process via a generalized Langevin equation, we show that velocity-dependent friction in fluids results from an intricate interplay of near-order structural effects and the non-Markovian behavior of the friction memory kernel. For complex fluids such as the model lubricant C40H82, the memory kernel exhibits a stretched-exponential long-time decay, which reflects the multitude of timescales of the system.
• Molecular Origin of Driving-Dependent Friction in Fluids M. Post, S. Wolf, and G. Stock, JCTC 2022, 18, 5, 2816-2825
While classical molecular dynamics (MD) simulations describe the motion of biomolecular systems in terms of usually thousands of atoms, their essential dynamics takes place on a way smaller, latent space, characterized by only few collective variables (CVs) \( \vec{x} \). These variables are chosen in such a way, that they encompass the statistical (structural) and dynamical features of these given systems: Biomolecular processes can then be described in terms of the distribution \( P(\vec{x}) \) an the corresponding free energy landscape \( \Delta G(\vec{x}) = - \mathrm{k}_B T \ln P(\vec{x}) \), visualizing the meta-stable states of the systems and the pathways in between these states and giving the bridge to coarse-grained models of these processes, like Langevin or Markov state models. A suitable choice of coordinates \( x \) is therefore paramount for a precise description of the biomolecular system at hand.
• Perspective: Identification of collective variables and metastable states of protein dynamics, F. Sittel and G. Stock, J. Chem. Phys 149, 150901 (2018)

Correlation based feature selection to identify collective motion

To interpret molecular dynamics simulations of biomolecular systems, systematic dimensionality reduction methods are commonly employed. Among others, this includes principal component analysis (PCA) and time-lagged independent component analysis (TICA), which aim to maximize the variance and the time scale of the first components, respectively. A crucial first step of such an analysis is the identification of suitable and relevant input coordinates (the so-called features), such as backbone dihedral angles and interresidue distances. As typically only a small subset of those coordinates is involved in a specific biomolecular process, it is important to discard the remaining uncorrelated motions or weakly correlated noise coordinates. This is because they may exhibit large amplitudes or long time scales and therefore will be erroneously considered important by PCA and TICA, respectively. To discriminate collective motions underlying functional dynamics from uncorrelated motions, the correlation matrix of the input coordinates is block-diagonalized by a clustering method. This strategy avoids possible bias due to presumed functional observables and conformational states or variation principles that maximize variance or time scales. Considering several linear and nonlinear correlation measures and various clustering algorithms, it is shown that the combination of linear correlation and the Leiden community detection algorithm yields excellent results for all considered model systems. These include the functional motion of T4 lysozyme to demonstrate the successful identification of collective motion, as well as the folding of the villin headpiece to highlight the physical interpretation of the correlated motions in terms of a functional mechanism.
• Correlation-Based Feature Selection to Identify Functional Dynamics in Proteins, G. Diez, D. Nagel and G. Stock, J. Chem. Theory Comput (2022)
Free energy landscape of HP35 via PCA using (a) Cartesian coordinates, (b) contact distances and (c) backbone dihedral angles (dPCA+), and (d) obtained from TICA, showing a clear structural resolution with dPCA in this case.

Principal component analysis - Cartesian vs. internal coordinates

One widely-used approach to systematically construct a low-dimensional set of CVs is called principal component analysis (PCA). Given some high-dimensional MD input data \( \vec{r} \), PCA describes the correlated motion of the system via their projection onto the eigenvectors of their covariance matrix \( \sigma_{\vec{r}_i \vec{r}_j} \) which account for the dynamics along the directions of maximum variance. While the Cartesian coordinates of all atoms in the system might be the straightforward choice for \( \vec{r} \), for flexible systems as a folding protein, this often leads to poor CVs, since it is not possible to remove their overall rotation due to mixing with the internal motions. Alternatively, internal coordinates, like dihedral angles and contact distances, can be suitable choices as inputs \( \vec{r} \): The former are valuable conformational descriptors that directly indicate whether the protein forms helices, sheets or loops. Due to their periodic nature, projections in circular space are ambiguous. We therefore proposed to use dPCA+, which exploit the fact that steric hindrances limit the full angular space such that natural cuts between sampled regions can be defined, allowing to perform PCA in a standard manner, without distortion errors and coordinate doubling as in the usual sin/cos-transformed coordinates of regular dPCA. The latter are well-suited to describe large-scale structural changes. Since the use of all possible distances between C\(_\alpha\)-atoms scales quadratically with the number of considered atoms, resulting in a numerically expensive analysis and moreover in highly correlated coordinates, we suggested to focus on distances between interresidue contacts of the protein that are present in the native state of a protein, since they have been shown to largely determine the folding pathways. We consider a contact as formed if the distance between the closest lying heavy atoms of each residue is less than \(0.45 \,\)nm and discard contacts between residues that are less than four residues apart, thereby omitting short-range contacts.
• Principal component analysis of molecular dynamics: On the use of Cartesian vs. internal coordinates, F. Sittel, A. Jain and G. Stock, J. Chem. Phys. 141, 014111 (2014)
• Principal component analysis on a torus: Theory and application to protein dynamics, F. Sittel, T. Filk, and G. Stock, J. Chem. Phys 147, 244101 (2017)
• Contact- and distance-based principal component analysis of protein dynamics M. Ernst, F. Sittel, and G. Stock, J. Chem. Phys. 143, 244114 (2015)

Density based clustering

Coming soon
The scheme of our machine learning algorithm (a) to identify essential internal coordinates shown by their feature importance (b) resulting from an iterative discard of unimportant features (c).

Learning the essential coordinates

Described as combinations of high-dimensional input coordinates, CVs tend to be hard to interpret as they do not necessarily point to the essential internal coordinates, i.e., specific interatomic distances or dihedral angles that are important for the considered process. Information on these coordinates, on the other hand, maybe provided by the metastable conformational states of the system, which yield a well-defined representation of the low free energy regions. Thus, using the data set of molecular coordinates (obtained from experiment or simulation) and an associated set of metastable conformational states (obtained from clustering the data), we can train a supervised machine learning model based on the learner XGBoost to assign unknown molecular structures to the set of metastable states. In this way, the model learns to determine the features of the molecular coordinates that are most important to discriminate the states. Using a new algorithm that exploits this feature importance via an iterative exclusion principle, we identify the essential internal coordinates (such as specific interatomic distances or dihedral angles) of the system, which are shown to represent versatile reaction coordinates that account for the dynamics of the slow degrees of freedom and explain the mechanism of the underlying processes. Moreover, these coordinates give rise to a free energy landscape that may reveal previously hidden intermediate states of the system.
• Machine Learning of Biomolecular Reaction Coordinates, S.Brandt, F. Sittel, M. Ernst, and G. Stock, J. Phys. Chem. Lett. 9, 2144 (2018)
Unfolding of the \(\alpha\)-helical state of Ala\(_{10}\). Though in equilibrium (c) the unfolded state is not sampled, the energy landscapes can still be estimated using non-equilibrium pulling (d,e).

PCA of nonequilibrium MD simulations

While PCA is routinely applied to equilibrium molecular dynamics (MD) simulations, it is less obvious how to extend the approach to nonequilibrium simulation techniques. This includes, e.g., the definition of the statistical averages employed in PCA, as well as the relation between the equilibrium free energy landscape \( \Delta G(\vec{x}) \) and energy landscapes \( \Delta \mathcal{G}(\vec{x}) \) obtained from nonequilibrium MD. As an example for a nonequilibrium method, "targeted MD" is considered which employs a moving distance constraint to enforce rare transitions along some biasing coordinates. The introduced bias can be described by a weighting function \(P(s) \), which provides a direct relation between equilibrium and nonequilibrium data, and thus establishes a well-defined way to perform PCA on nonequilibrium data. While the resulting distribution \( P(\vec{x}) \) and energy \( \Delta G \propto \ln P \) will not reflect the equilibrium state of the system, the nonequilibrium energy landscape \(\Delta \mathcal{G}(\vec{x}) \) may directly reveal the molecular reaction mechanism. Although the formulation is in principle exact, its practical use depends critically on the choice of the biasing coordinates, which should account for a naturally occurring motion between two well-defined end-states of the system.
• Principal component analysis of nonequilibrium molecular dynamics simulations, M. Post, S. Wolf, and G. Stock, J. Chem. Phys 150, 101063 (2019)
Computer simulations have become indispensable tools for exploring the dynamics of proteins. However, as it is neither possible nor desirable to follow the motion of a complex molecule along its 3N atomic coordinates, we need methods that can fully realize the potential of the simulations. One of the most important driving force for the modeling and analysis of MD simulation data are Markov state models (MSM), which model the often bewildering dynamics of a protein by memoryless, probabilistic jumps between its metastable configurations. The key assumption behind Markov state models is that the dynamics of the system can be approximated by a Markov chain meaning that the actual state of the system \(X\) does only depend on its predecessor \( p( X_{T+1}| X_0, \dots, X_T) = p(X_{T+1}| X_{T}) \). Therefore, a major challenge in Markov state modeling is to find such states \(X\) for which this Markov property is fulfilled which requires different strategies to reduce the dimensionality of the data while retaining the dynamical information.
• Perspective: Identification of collective variables and metastable states of protein dynamics, Florian Sittel and Gerhard Stock, J. Chem. Phys. 149, 150901 (2018)
• Dynamical coring of Markov state models, Daniel Nagel, Anna Weber, Benjamin Lickert and Gerhard Stock, J. Chem. Phys. 150, 094111 (2019)
A popular approach to analyze complex biomolecular systems is to define a low-dimensional reaction coordinate which aims for an appropriate description of the essential collective dynamics. Assuming a separation of time scales between those coordinates and the neglected orthogonal degrees of freedom, the Markovian Langevin equation represents a powerful framework to investigate and interpret the observed dynamics. We have developed a data-driven Langevin equation (dLE) algorithm to estimate multidimensional Langevin fields from MD data. Only based on local information, the dLE allows for the interpretation of enhanced sampling data to predict long time dynamics like transition times. Based on dLE studies we proposed a practical method to construct an analytically defined global model of structural dynamics. This approach employs an “empirical valence bond”-type model which can cover multidimensional free energy landscapes as well as an approximate description of the friction field estimated by the dLE. Adopting alanine dipeptide and a three-dimensional model of heptaalanine as simple examples, the resulting Langevin model reproduced the results of the underlying all-atom simulations. For further applications, analytically defined models can be used to investigate the dependence of the system on parameter changes and to predict the effect of site-selective mutations on the dynamics.
• Global Langevin model of multidimensional biomolecular dynamics, Norbert Schaudinnus, Benjamin Lickert, Mithun Biswas and Gerhard Stock J. Chem. Phys. 145, 184114 (2016)
• Multidimensional Langevin Modeling of Nonoverdamped Dynamics, Norbert Schaudinnus, Björn Bastian, Rainer Hegger, and Gerhard Stock, Phys. Rev. Lett. 115,050602 (2015)

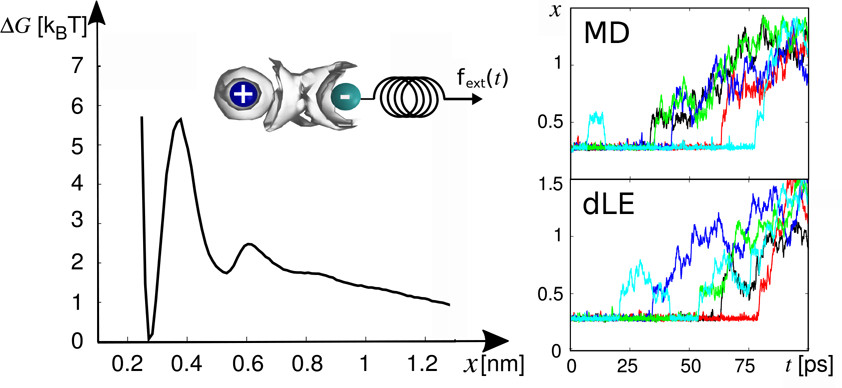
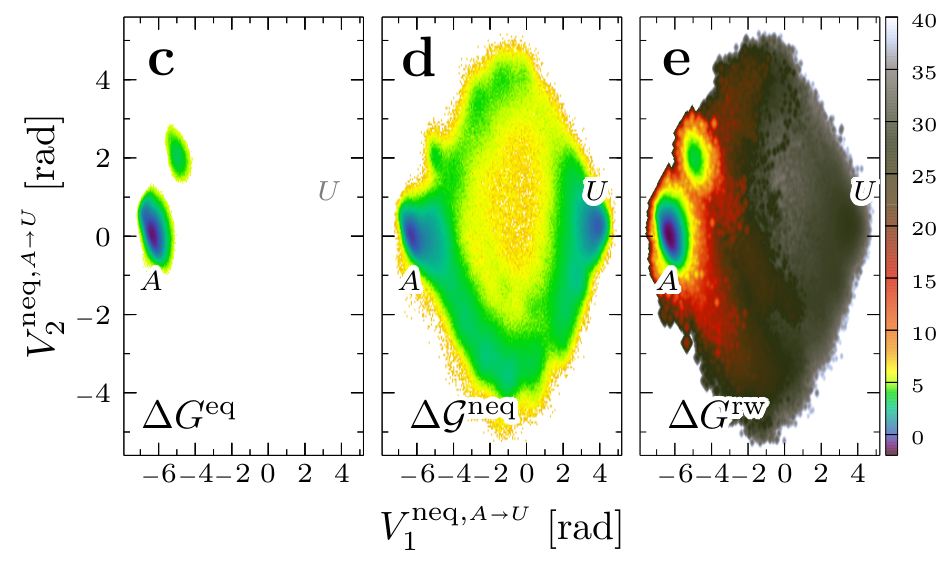
Data-driven Langevin modeling of nonequilibrium processes

Given nonstationary data from molecular dynamics simulations, a Markovian Langevin model is constructed that aims to reproduce the time evolution of the underlying process. While at equilibrium the free energy landscape is sampled, nonequilibrium processes can be associated with a biased energy landscape, which accounts for finite sampling effects and external driving. When the data-driven Langevin equation (dLE) approach [Phys. Rev. Lett. 2015, 115, 050602] is extended to the modeling of nonequilibrium processes, an efficient way to calculate multidimensional Langevin fields is outlined. The dLE is shown to correctly account for various nonequilibrium processes, including the enforced dissociation of sodium chloride in water, the pressure-jump induced nucleation of a liquid of hard spheres, and the conformational dynamics of a helical peptide sampled from nonstationary short trajectories.
• Principal component analysis of nonequilibrium molecular dynamics simulations, B. Lickert, S. Wolf, and G. Stock, J. Phys. Chem. B 125, 8125 (2021)
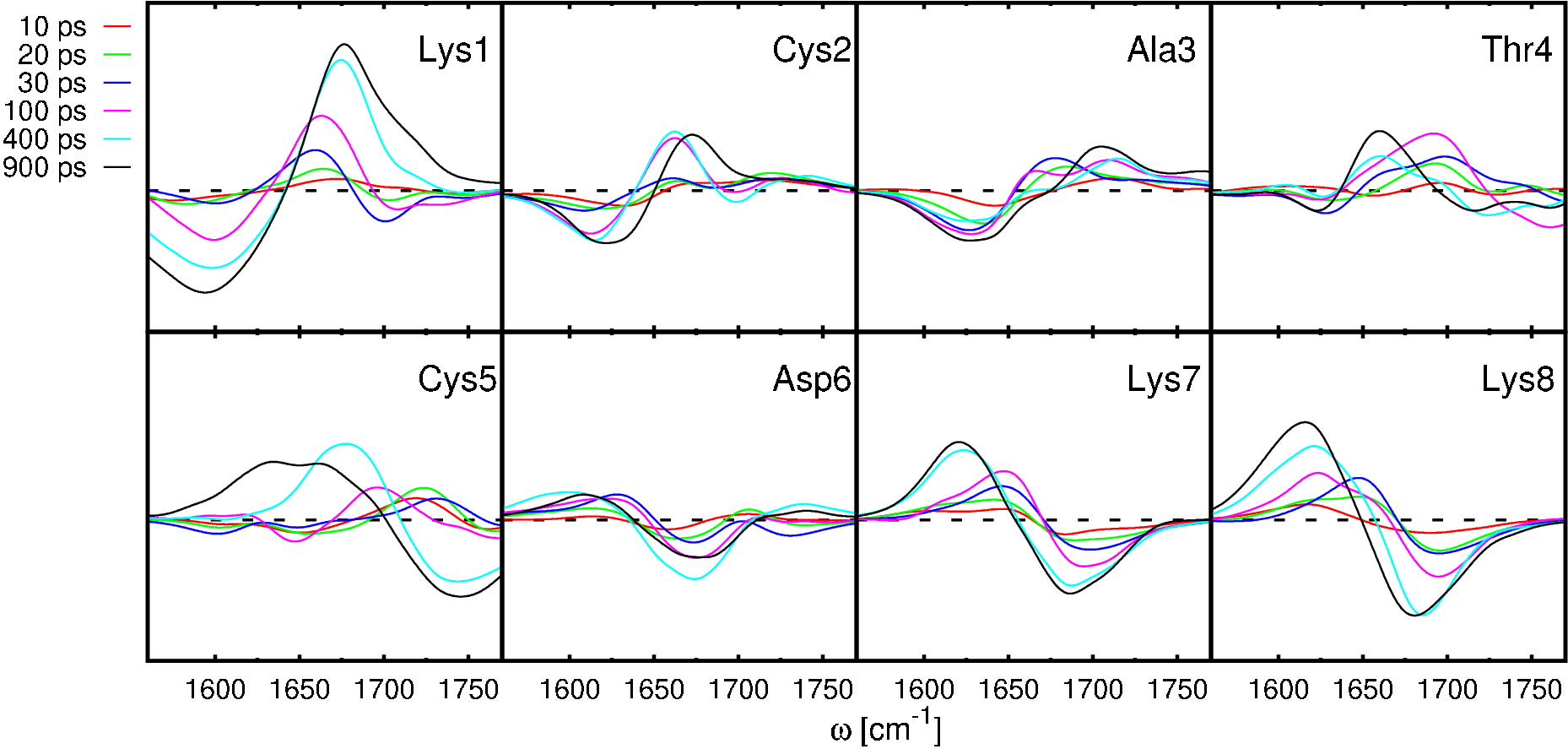
Modern techniques of infrared spectroscopy, in particular multidimensional and time-resolved version of it, have opened the way to monitor secondary structure and dynamics of polypeptides and proteins. In particular the amide I band, reflecting the backbone C=O stretching vibration, has been found to yield structural information. To obtain a first principles description of the amide I vibrational spectrum of peptides in aqueous solution, we pursue a quantum-classical approach which consists of a classical molecular dynamics simulation of the conformational distribution of the system, density functional theory calculations of the conformation-dependent and solvent-induced frequency fluctuations, and a semiclassical description of the vibrational line shapes.

Vibrational Spectroscopic Map, Vibrational Spectroscopy, and Intermolecular Interaction

Vibrational spectroscopy is an essential tool in chemical analyses, biological assays, and studies of functional materials. Over the past decade, various coherent nonlinear vibrational spectroscopic techniques have been developed and enabled researchers to study time-correlations of the fluctuating frequencies that are directly related to solute−solvent dynamics, dynamical changes in molecular conformations and local electrostatic environments, chemical and biochemical reactions, protein structural dynamics and functions, characteristic processes of functional materials, and so on. In order to gain incisive and quantitative information on the local electrostatic environment, molecular conformation, protein structure and interprotein contacts, ligand binding kinetics, and electric and optical properties of functional materials, a variety of vibrational probes have been developed and sitespecifically incorporated into molecular, biological, and material systems for time-resolved vibrational spectroscopic investigation. However, still, an all-encompassing theory that describes the vibrational solvatochromism, electrochromism, and dynamic fluctuation of vibrational frequencies has not been completely established mainly due to the intrinsic complexity of intermolecular interactions in condensed phases. In particular, the amount of data obtained from the linear and nonlinear vibrational spectroscopic experiments has been rapidly increasing, but the lack of a quantitative method to interpret these measurements has been one major obstacle in broadening the applications of these methods. Among various theoretical models, one of the most successful approaches is a semiempirical model generally referred to as the vibrational spectroscopic map that is based on a rigorous theory of intermolecular interactions. Recently, genetic algorithm, neural network, and machine learning approaches have been applied to the development of vibrational solvatochromism theory. In this review, we provide comprehensive descriptions of the theoretical foundation and various examples showing its extraordinary successes in the interpretations of experimental observations. In addition, a brief introduction to a newly created repository Web site (http://frequencymap.org) for vibrational spectroscopic maps is presented. We anticipate that a combination of the vibrational frequency map approach and state-of-the-art multidimensional vibrational spectroscopy will be one of the most fruitful ways to study the structure and dynamics of chemical, biological, and functional molecular systems in the future.
• Vibrational Spectroscopic Map, Vibrational Spectroscopy, and Intermolecular Interaction, C. R. Baiz, B. Blasiak, J. Bredenbeck, M. Cho, J-H Choi, S. A. Corcelli, A. G. Dijkstra, C-J Feng, S. Garrett-Roe, N-Hi Ge, M. W. D. Hanson-Heine, J. D. Hirst, T. L. C. Jansen, K. Kwac, K. J. Kubarych, C. H. Londergan, H. Maekawa, M. Reppert, S. Saito, S. Roy, J. L. Skinner, G. Stock et al, Chemical Reviews 120 (15), 7152 (2020) 15

Real time observation of ultrafast peptide conformational dynamics: MD simulation vs. IR experiment

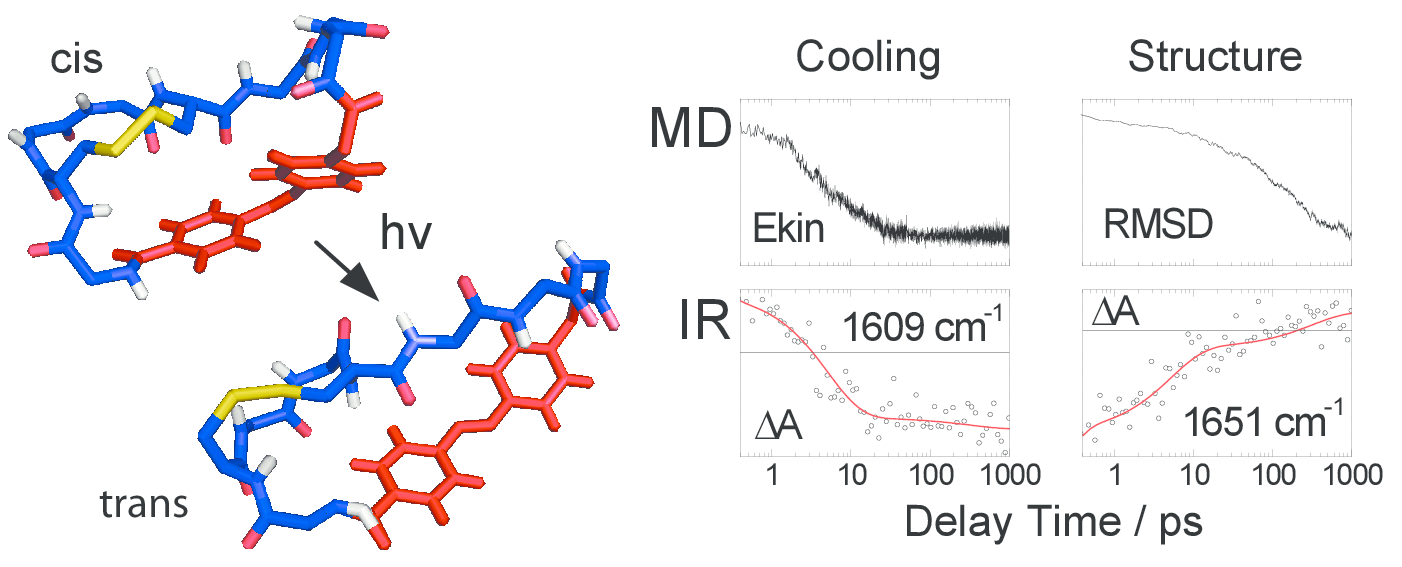
Employing nonequilibrium molecular dynamics (MD) simulations and transient infrared (IR) spectroscopy, a joint theoretical/experimental study on a water-soluble photoswitchable octapeptide designed by Renner et al. [Biopolymers 63, 382 (2002)] is presented. The simulations predict the cooling of the hot photoproducts on a time scale of 7 ps and complex conformational rearrangements ranging from a few picoseconds to several nanoseconds. The experiments yield a dominant fast relaxation time of 5 ps, which is identified as the cooling time of the peptide in water and also accounts for initial conformational changes of the system. Moreover, a weaker component of 300 ps is found, which reflects the overall conformational relaxation of the system. The virtues and the limitations of the joint MD/IR approach to describe biomolecular conformational rearrangements are discussed.
• Real Time Observation of Ultrafast Peptide Conformational Dynamics: Molecular Dynamics Simulation vs Infrared Experiment, Norbert P. H. Nguyen, H. Staudt, J. Wachtveitl, and G. Stock, J. Phys. Chem. B 115, 13084 (2011)

Simulation of transient infrared spectra of a photoswitchable peptide

In transient infrared (IR) experiments, a molecular system may be photoexcited in a nonstationary conformational state, whose time evolution is monitored via IR spectroscopy with high temporal and structural resolution. As a theoretical formulation of these experiments, this work derives explicit expressions for transient one- and two-dimensional IR spectra and discusses various levels of approximation and sampling strategies. Adopting a photoswitchable octapeptide in water as a representative example, nonequilibrium molecular dynamics simulations are performed and the photoinduced conformational dynamics and associated IR spectra are discussed in detail. Interestingly, it is found that the time scales of dynamics and spectra may differ from residue to residue by up to an order of magnitude. Considering merely the cumulative spectrum of all residues, the contributions of the individual residues largely compensate each other, which may explain the surprisingly small frequency shifts and short photoproduct rise times found in experiment. Even when a localized amide I mode is probed (e.g., via isotope labelling), the vibrational frequency shift is shown to depend in a complicated way on the conformation of the entire peptide as well as on the interaction with the solvent. In this context, various issues concerning the interpretation of transient IR spectra and conformational dynamics in terms of a few exponential time scales are discussed.
• Simulation of transient infrared spectra of a photoswitchable peptide, M. Kobus, M. Lieder, P. H. Nguyen, and G. Stock, Chem. Phys. 135, 225102 (2011)
Left: Free energy landscape ΔG (φ, ψ) (in kJ/mol) along the inner backbone dihedral angles φ and ψ of the Aib peptide, obtained for 220 and 300K.
Right: (A) Short-time evolution of the total C=O frequency fluctuation  correlation function at 220 K (red) and 300 K (green). The curves are fitted by an exponential function, the weight (green) and decay  time τ (red) of which are shown in panel (B) as a function of temperature. The resulting total homogeneous dephasing rate (red) is shown in (C) together with the antidiagonal width of the 2D-IR spectra (green).

Infrared signatures of the peptide dynamical transition

Recent two-dimensional infrared (2D-IR) experiments on a short peptide 310-helix in chloroform solvent [Backus et al., J. Phys. Chem. B 113, 13405 (2009)] revealed an intriguing temperature dependence of the homogeneous line width, which was interpreted in terms of a dynamical transition of the peptide. To explain these findings, extensive molecular dynamics simulations at various temperatures were performed in order to construct the free energy landscape of the system. The study recovers the familiar picture of a glass-forming system, which below the glass transition temperature Tg is trapped in various energy basins, while it diffuses freely between these basins above Tg. In fact, one finds at Tg≈ 270 K a sharp rise of the fluctuations of the backbone dihedral angles, which reflects conformational transitions of the peptide. The corresponding C=O frequency fluctuations are found to be a sensitive probe of the peptide conformational dynamics from femtosecond to nanosecond time scales and lead to 2D-IR spectra that qualitatively match the experiment. The calculated homogeneous line width, however, does not show the biphasic temperature dependence observed in experiment. The discrepancy appears to be caused by the inappropriate modeling of the frequency shift of the chloroform solvent, which indicates the importance of solvent fluctuations for the peptide dynamical transition.
• Infrared signatures of the peptide dynamical transition: A molecular dynamics simulation study, M. Kobus, P. H. Nguyen, and G. Stock, J. Chem. Phys. 133, 034512 (2010)

Nonadiabatic Vibrational Dynamics in the HCO\(_2^- \cdot \) H\(_2\)O Complex

Based on extensive ab initio calculations and the time-propagation of a 6-dimensional nuclear Schrödinger equation, we study the vibrational relaxation dynamics and resulting spectral signature of the OH stretch vibration of a hydrogen-bonded complex, HCO\(_2^- \cdot \) H\(_2\)O. Despite its smallness, it has been shown experimentally by Johnson and coworkers that the gas-phase IR spectra of these types of complexes exhibits much of the complexity commonly observed for hydrogen bonded systems, i.e., a significant red shift together with an extreme broadening and a pronounced substructure of the OH stretch vibration, reflecting its very strong anharmonicity. Employing an adiabatic separation of timescales between the three intramolecular high-frequency modes of the water molecule and the three most important intermolecular low-frequency modes of the complex, we identify a vibrational conical intersection seam that connects the OH stretch vibration to the HOH bend overtone. The conical intersection results in a coherent population transfer between the two states, the first step of which being ultrafast with 60~fs and irreversible, as one would intuitively predict based on the knowledge accumulated for ultrafast photophysical processes between electronic potential energy surfaces. The density of states of our model is large enough to also realistically describe the subsequent incoherent relaxation of vibrational energy into the HOH bend and ground state. However, despite the fact that no conical intersection connects to these states, that relaxation is only insignificantly slower, as opposed to what would be expected in the electronic case. The underlying adiabatic picture hence constituted only a rather poor approximation of vibrational dynamics. We identify the smaller effective mass difference as the major difference between a vibrational and the more common electronic adiabatic approximation.
• Nonadiabatic Vibrational Dynamics in the HCO\(_2^- \cdot \) H\(_2\)O complex, P. Hamm,and G. Stock J. Chem. Phys. 143, 134308 (2015)

Vibrational Conical Intersections as a Mechanism of Ultrafast Vibrational Relaxation

Presenting true crossings of adiabatic potential energy surfaces, conical intersections are a paradigm of ultrafast and efficient electronic relaxation dynamics. The same mechanism is shown to apply also for vibrational conical intersections, which may occur when two high-frequency modes (such as OH stretch vibrations) are coupled to low-frequency modes (such as hydrogen bonding modes). By derivation of a model Hamiltonian and its parameterization for a concrete example, malonaldehyde, the conditions that such intersections occur are identified and the consequences for the vibrational dynamics and spectra are demonstrated.
• Vibrational Conical Intersections as a Mechanism of Ultrafast Vibrational Relaxation, P. Hamm and G. Stock Phys. Rev. Lett. 109, 173201 (2012)

Ultrafast nonadiabatic photoreactions

A quantum dynamical description

Modern pulsed laser techniques provide an ultrafast camera that allows us to explore the motion of atoms at a femtosecond (10-15s) time resolution. The fascination of femtosecond chemistry lies in the possibility to directly observe elementary chemical reactions. For example, femtosecond experiments have shed light on the primary electron transfer process in the bacterial photoreaction center and have witnesses the making and braking of hydrogen bonds in biopolymers.
State-of-the-art femtosecond experiments generate an enormous amount of data, which require a careful theoretical analysis. However, neither straightforward quantum mechanics nor simple classical modeling is typically suited to describe the femtosecond dynamics and spectroscopy of complex systems. The theory therefore is challenged to develop new strategies. Approaches pursued in this group include the development of multidimensional reduced quantum-models and of new mixed quantum-classical concepts. Hereby the ultimate goal is an truly microscopic understanding of the underlying physics and, of course, the pleasure play with new theoretical ideas.

As an example, the upper picture shows a recently proposed model of the photoinduced cis-trans isomerization of retinal in rhodopsin, representing the first step in vision. Shown are two-dimensional potential-energy surfaces of the ground and excited electronic states. The photoreaction is initiated via vertical excitation by a pump laser pulse, which prepares a vibrational wave packet on the excited electronic state. The wave packet, shown in the right picture, is seen to bifurcate at a conical intersection of the adiabatic surfaces, whereby the photoproduct is formed with high efficiency and within only 200 fs such as the making and breaking of chemical bonds in real time, that is, on a femtosecond time scale.
• Femtosecond time-resolved spectroscopy of the dynamics at conical intersections, G. Stock and W. Domcke, Conical Intersections, eds: W. Domcke, D. R. Yarkony, and H. Koppel, (World Scientific, Singapore, 2003)

A classical description

Since the birth of quantum theory there has been a considerable interest in the transition from quantum to classical mechanics. Because the two formulations are given in a different theoretical framework (nonlinear classical trajectories vs. expectation values of linear operators), this transition is far more involved than the naive limit h → 0  suggests. Furthermore, many quantum-mechanical systems and phenomena have no obvious classical analog. For example, it is not obvious how to extend a trajectory simulation running on a single Born-Oppenheimer potential-energy surface to a classical description of nonadiabatic processes taking place on several coupled electronic potential-energy surfaces.
In this research project, we are concerned with various theoretical formulations that allow us to treat nonadiabatic quantum dynamics in a classical description. We are interested in fundamental aspects of semiclassical dynamics as well as in the development of practical mixed quantum-classical techniques which are capable of describing the dynamics of complex molecular systems. Considering multidimensional model problems describing photoinduced electron transfer, internal-conversion via conical intersections and nonadiabatic photoisomerization, the methods employed include mean-field, surface-hopping, and the quantum-classical Liouville formulations. In particular, we are interested in the mapping approach to nonadiabatic quantum dynamics. Going beyond the usual quasiclassical approximation, the formulation allows us to characterize the classical phase space and the periodic orbits of a nonadiabatic system and to achieve a true semiclassical treatment of nonadiabatic dynamics via an initial-value representation.
As an example, we consider a two-state three-mode model of nonadiabatic cis-transphotoisomerization. The figure compares the quantum-mechanical (left) and quasiclassical mapping (right) probability densities of the time-dependent wave packet along isomerization coordinate ϕ, projected on the S1 (upper panel) and S0 (lower panel) adiabatic electronic state, respectively. The classical approach is seen to be in good agreement with the quantum calculation, it facilitates the interpretation of the diffuse wave function in terms of irregular vibronic periodic orbits, and allows us to extend the study to many (up to 104) vibrational degrees of freedom.
• Classical Description of Nonadiabatic Quantum Dynamics, G. Stock and M. Thoss, Adv. Chem. Phys. 131, 243-375 (2005)

Maximum Caliber

We show how to apply a general theoretical approach to nonequilibrium statistical mechanics, called Maximum Caliber, originally suggested by E. T. Jaynes 30 years ago, to a problem of two-state dynamics. Maximum Caliber is a variational principle for dynamics in the same spirit that Maximum Entropy is a variational principle for equilibrium statistical mechanics. The central idea is to compute a dynamical partition function, a sum of weights over all microscopic paths, rather than over microstates. We illustrate the method on the simple problem of two-state dynamics, A ↔ B, first for a single particle, then for M articles. Maximum Caliber gives a unified framework for deriving all the relevant dynamical properties, including the microtrajectories and all the moments of the time-dependent probability density. While it can readily be used to derive the traditional master equation and the Langevin results, it goes beyond them in also giving trajectory information. For example, we derive the Langevin noise distribution, rather than assuming it. As a general approach to solving nonequilibrium statistical mechanics dynamical problems, Maximum Caliber has some advantages:
  • It is partition-function-based, so we can draw insights from similarities to equilibrium statistical mechanics,
  • it is trajectory-based, so it gives more dynamical information than population-based approaches like master equations; this is particularly important for few-particle and single-molecule systems,
  • it gives an unambiguous way to relate flows to forces, which has traditionally posed challenges, and
  • like Maximum Entropy, it may be useful for data analysis, specifically for time-dependent phenomena.
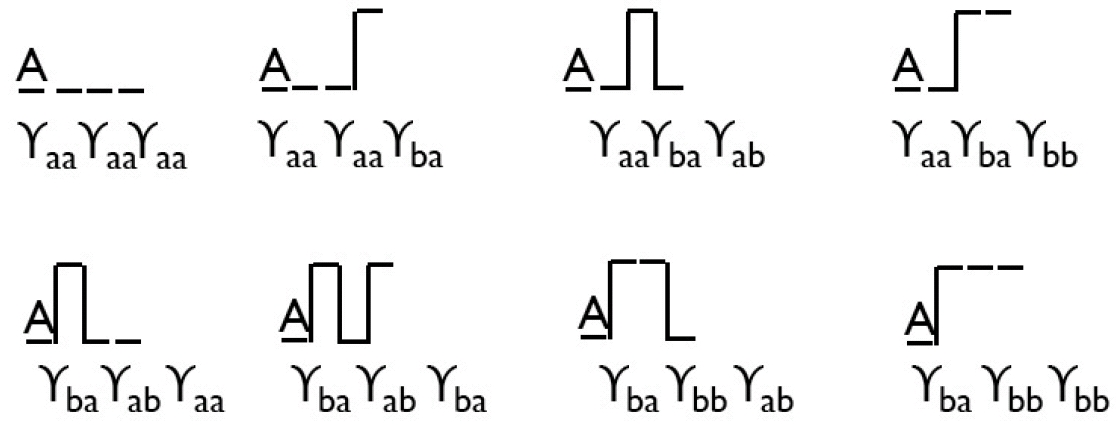
Graphical representation of the dynamical partition function of a two-state system, showing all possible trajectories for N=3 time steps for a system stating in A.
• Maximum Caliber: A variational approach applied to two-state dynamics, G. Stock, K. Ghosch, and K. A. Dill, J. Chem. Phys. 128, 194102-194102-12 (2008)
• Maximum caliber inference of nonequilibrium processes, M. Otten, and G. Stock, J. Chem. Phys. 133, 034119 (2010)
• Inferring Transition Rates of Networks from Populations in Continuous-Time Markov Processes, P. D. Dixit, A. Jain, G. Stock, and K. A. Dill J. Chem. Theory Comput. 11, 5464 (2015)